Chapter 6 Problem Solutions
James R. Martin, Ph.D., CMA
Professor Emeritus, University of South Florida
Chapter 6 | MAAW's Textbook Table of Contents

SOLUTION 6-2
1. Direct method:
P1 = 500,000 + (280/390)(S1) + (1,000/1,700)(S2)
= 500,000 + (280/390)(100,000) + (1,000/1,700)(200,000)
= 689,441.93
P2 = 300,000 + (110/390)(S1) + (700/1,700)(S2)
= 300,000 + (110/390)(100,000) + (700/1,700)(200,000)
= 410,558.07
Note: 689,441.93 + 410,558.07 = $1,100,000 total direct costs.
2. Step-down method:
S2 is closed first, therefore S2 = 200,000
S1 = 100,000 + (100/1,800)(S2)
= 100,000 + (100/1,800)(200,000) = 111,111.11
P1 = 500,000 + (280/390)(S1) + (1,000/1,800)(S2)
= 500,000 + (280/390)(111,111.11) + (1,000/1,800)(200,000)
= 690,883.19
P2 = 300,000 + (110/390)(S1) + (700/1,800)(S2)
= 300,000 + (110/390)(111,111.11) + (700/1,800)(200,000)
= 409,116.81
Note: 690,883.19 + 409,116.81 = $1,100,000
3. Reciprocal method:
S1 = 100,000 + (100/2,000)(S2)
S2 = 200,000 + (10/400)(S1) + (200/2,000)(S2)
P1 = 500,000 + (280/400)(S1) + (1,000/2,000)(S2)
P2 = 300,000 + (110/400)(S1) + (700/2,000)(S2)
Substitute S1 into the equation for S2 to solve for S2.
S2 = 200,000 + (10/400)(S1) + (200/2,000)(S2)
S2 = 200,000 + (10/400)[100,000 + (100/2,000)(S2)] + (200/2,000)(S2)
= 200,000 + 2,500 + (.00125)(S2) + (.1)(S2)
= 225,312.94
Then solve for S1, P1 and P2.
S1 = 100,000 + (100/2,000)(225,312.94)
= 111,265.65
P1 = 500,000 + (280/400)(111,265.65) + (1,000/2,000)(225,312.94)
= 690,542.43
P2 = 300,000 + (110/400)(111,265.65) + (700/2,000)(225,312.94)
= 409,457.58
Note: 690,542.43 + 409,457.58 = 1,100,000
SOLUTION 6-3
1. Direct method:
P1 = 6,000,000 + (1,000/1,500)(S1) + (800/1,200)(S2)
= 6,000,000 + (1,000/1,500)(500,000) + (800/1,200)(1,000,000)
= 7,000,000
P2 = 2,000,000 + (500/1,500)(S1) + (400/1,200)(S2)
= 2,000,000 + (500/1,500)(500,000) + (400/1,200)(1,000,000)
= 2,500,000
Note: 7,000,000 + 2,500,000 = $9,500,000 total direct costs.
2. Step-down method:
S2 is closed first, therefore S2 = 1,000,000
S1 = 500,000 + (1,000/2,200)(S2)
= 500,000 + (1,000/2,200)(1,000,000)
= 954,545.45
P1 = 6,000,000 + (1,000/1,500)(S1) + (800/2,200)(S2)
= 6,000,000 + (1,000/1,500)(954,545.45) + (800/2,200)(1,000,000)
= 7,000,000
P2 = 2,000,000 + (500/1,500)(S1) + (400/2,200)(S2)
= 2,000,000 + (500/1,500)(954,545.45) + (400/2,200)(1,000,000)
= 2,500,000
Note: 7,000,000 + 2,500,000 = 9,500,000
3. Reciprocal method:
S1 = 500,000 + (80/1,600)(S1) + (1,000/2,400)(S2)
S2 = 1,000,000 + (20/1,600)(S1) + (200/2,400)(S2)
P1 = 6,000,000 + (1,000/1,600)(S1) + (800/2,400)(S2)
P2 = 2,000,000 + (500/1,600)(S1) + (400/2,400)(S2)
Computer recommended for solution.
S1 = 1,010,830
S2 = 1,104,693
P1 = 7,000,000
P2 = 2,500,000
SOLUTION 6-4
1. b
2. c
3. d. B&O is closed first because it provides 9.8% (880/9,000) of its’ service to P&M while P&M provides only 1% (10/1,000) of it's service to B&O.
4. a since B&O receives no allocation from P&M,
5. c
6. d
7. b
8. a
9. b
10. c
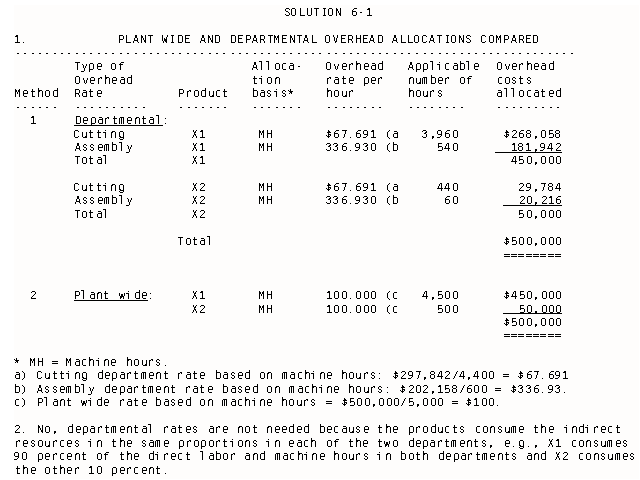
11. c because X1 and X2 consume the same proportion of machine hours (20% and 80% respectively) in each department.
12. d
SOLUTION 6-5
1. a
2. c
3. a
4. c
5. d
6. d
7. d
8. b
SOLUTION 6-6
1. d
2. b
3. a
4. c
5. e Use materials as an allocation basis in P1 and machine hours in P2.